Albert Einstein, lui-même à compris très rapidement la puissance et la magie que les intérêts composés peuvent offrir. Voici une de ses célèbres citations.
« L’intérêt composé est la huitième merveille du monde. Celui qui peut bien comprendre l’intérêt composé en bénéficie, celui qui ne le comprend pas… le paie. »
Albert Einstein, lauréat du prix Nobel et physicien
Bien qu’il n’existe pas une preuve formelle que cette situation soit, à la base, attribuée à Mr. Einstein, ce qui est certain, c’est le pouvoir de l’intérêt composé et notre incapacité à bien le comprendre en tant qu’être humain alpha. Mais pourquoi avons-nous de la peine à comprendre son fonctionnement ?
Fonction linéaire et exponentielle
En règle générale, la plupart des gens n’ont aucune peine de comprendre et visualiser des comportements linéaires. Cela est sûrement dû au fait que la plupart des gens qui nous entourent adoptent des comportements linéaires tout comme la plupart des phénomènes naturels. Prenons quelques exemples de phénomènes linéaires :
- Virement mensuel sur ton compte d’épargne : tu vires 300.- CHF chaque mois. Sur une année, tu auras donc viré 3’600.- CHF (12 x 300.- CHF).
- Consommation d’essence : ta voiture consomme 7 litres/100 km en moyenne. Après 800 km, tu auras donc consommé 56 litres (8 x 7 litres).
Je pense que le concept est simple et évident à comprendre. En langage mathématique, c’est d’autant plus simple et évident :
f(x) -> ax , où « a » est un nombre réel appelé coefficient de la fonction linéaire (ou de proportionnalité)
– Si « a » > 0, « f » grandira
– Si « a » < 0, "f" diminuera
Bref, c’est très simple et basic. Si on devait représenter ce comportement de manière graphique, on pourrait avoir quelque chose de ressemblant à ceci :
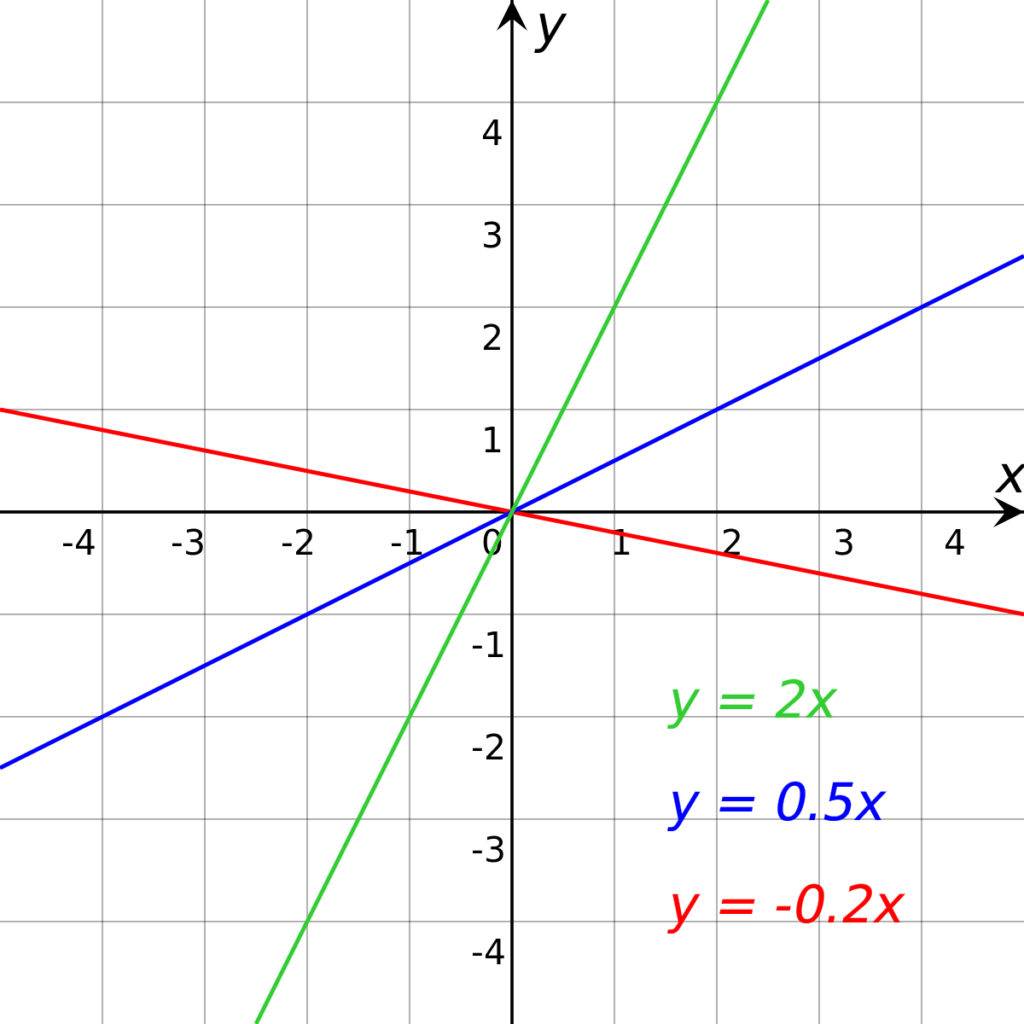
Cependant, les intérêts composés suivent une fonction exponentielle. Voici quelques exemples :
- Les bactéries possèdent une croissance exponentielle (elles se démultiplient.)
- Le nombre d’habitants sur la planète subit une croissance exponentielle (environ 1.12 % an)1.
- La capitalisation de l’argent sur un compte en banque (c’est ce qui nous intéresse.)
En langage mathématique, c’est un peu plus compliqué et je vais vous épargner les différentes représentations possibles ainsi que les propriétés de ce type de fonction. Une visualisation sera plus parlante :
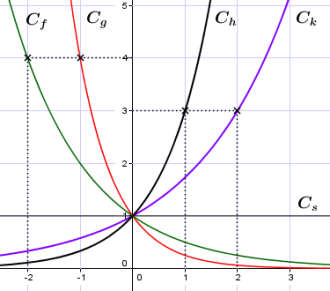
On peut donc imager une fonction exponentielle comme une croissance en % qui est constante avec le même facteur multiplicatif. Prenons le cas qui nous intéresse, le taux d’intérêt d’un compte en banque. Voici les valeurs
Exemple avec un compte en banque
Rentrons dans le vif du sujet avec cet exemple basique.
- Capital sur le compte au 1er janvier de l’an 0 : 1000.- CHF
- Taux d’intérêt du compte : 5.0 %
- Calcul d’intérêt : annuel
- Versements annuels : 0.- CHF
- Période : = 1 année
On est donc dans un cas très basic et certes un peu théorique, car il n’existe pas des comptes d’épargne à 5 % d’intérêt en Suisse et il est rare que l’on ne verse pas d’argent sur ce compte durant 45 ans. De plus, il faudrait également soustraire les frais de gestion du compte. Mais le but ici et de comprendre la puissance des intérêts composés.
Question : quel sera le montant sur ce compte dans 45 ans ?
Pour calculer ceci de manière dynamique, la formule serait la suivante : f(x) = 1000 * 1.050x , x étant le nombre d’années. En entrant cette fonction dans Excel, on aura les valeurs suivantes :
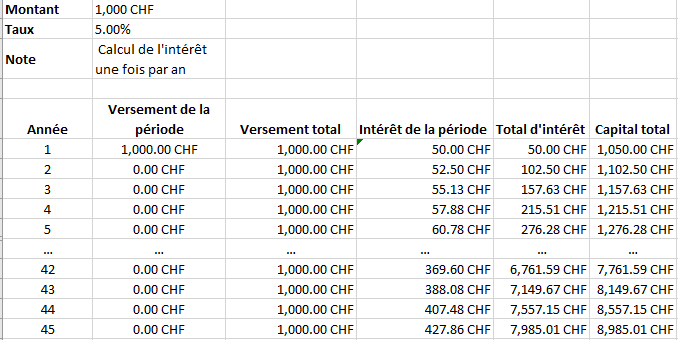
Ce qu’il faut comprendre ici, c’est l’évolution exponentielle des intérêts. Comme le montre la colonne « intérêt de la période« , chaque année, le placement génère plus d’intérêts. Après 5 ans, le placement initial de 1000.- CHF nous rapporte 60.78 CHF d’intérêt alors qu’après 45 ans, toujours sans avoir fait un seul versement supplémentaire, notre placement de 1000.- CHF nous rapporte 427.86 CHF d’intérêts ! Cela est dû au fait que les intérêts générés chaque année s’ajoutent au 1000.- CHF initiaux et que le taux d’intérêt (ou de rendement) reste identique. Au final, notre placement de 1000.- CHF permet d’avoir, après 45 ans et aux conditions hypothétiques théoriques présentées, 8’895.01 CHF !
Ces chiffres peuvent paraître incroyables, mais c’est bel et bien ceci la magie des intérêts composés. Certes, on ne trouve pas en Suisse un compte d’épargne ou salaire avec un taux de 5.0 %, mais cela peut s’avérer vrai dans le cas de placement en bourse. À noter que dans la vraie vie, le calcul des intérêts peut se faire à chaque mois, semestre, trimestre ou annuellement. Cela influence également légèrement le calcul.
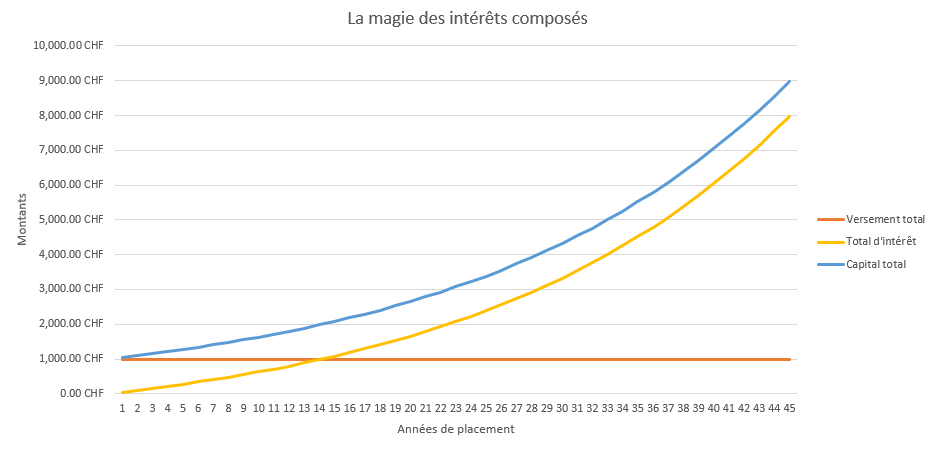
On voit très bien sur ce graphique représentant le capital total sur le compte en fonction des années, que la courbe n’est pas linéaire, mais bel et bien exponentielle. Plus longtemps tu vas laisser l’argent sur ce compte, plus les intérêts annuels générés seront importants ! La courbe (ligne du coup) orange montre bien qu’il n’y a pas eu d’autres versements durant toutes ces années et les deux autres courbes ont bien évidemment une croissance plus ou moins similaire puisque le capital total (courbe bleue) est composé du solde initial additionné des intérêts cumulés chaque année.
Même calcul avec un versement annuel
La simulation précédente représente un cas où l’on n’ajoute pas de capitaux durant 45 ans. Imagine le calcul si tu verses 1000.- / an sur ce compte, et cela, pendant 45 ans. On prend l’hypothèse que ce compte avait déjà 1000.- CHF au début. Sans intérêt, tu auras donc 46’000.- CHF sur ce compte (1000.- CHF initial + 45 x 1000.- CHF). Pour simplifier le calcul, on va dire que tu verses 1’000.- CHF chaque 1er janvier et que les intérêts sont calculés une fois par an au 31 décembre.
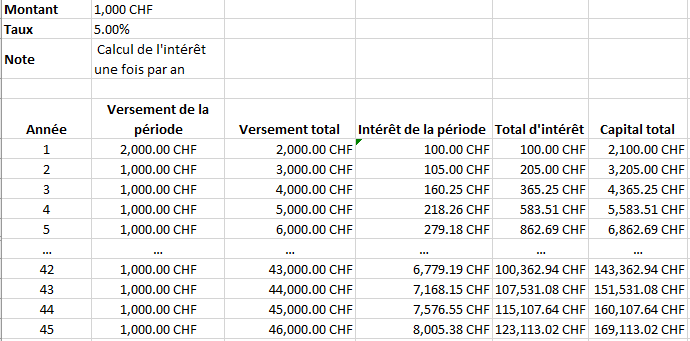
Impressionnant, n’est-ce pas ? Voici ce que sa donne visuellement :
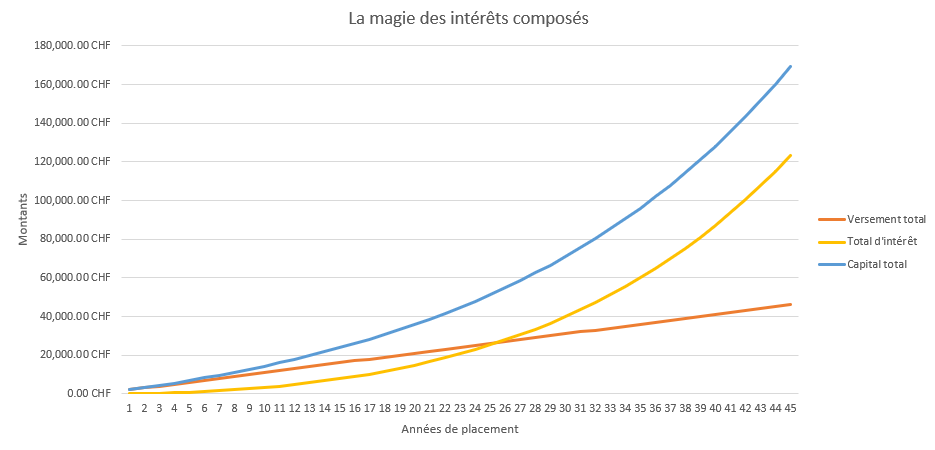
Toujours pas convaincu ? Un dernier calcul pour la route
Prenons l’exemple de Tom. Tom a 20 ans et vient tout juste de commencer à travailler. Son salaire n’étant pas très élevé, il ne peut pas mettre plus que 50.- CHF par mois de côté. Cependant, Tom a un ami plus agé qui lui a expliqué à maintes reprises l’importance de commencer à placer son argent le plus tôt possible. Tom demande à son ami de l’aider à placer 50.- CHF/mois sur un 3a investi à 60 % en action. D’après les moyennes et diverses étude de l’institution où Tom place son argent, le rendement moyen annualisé est de 3.5 % après avoir déduit tous les frais.
Combien Tom aura sur ce compte lorsqu’il prendra sa retraite, disons à 65 ans ?
Il a donc investi 50.- CHF/mois pendant 45 ans, soit 600.- CHF/an à un taux annualisé moyen de 3.5 %. Au total, il aura versé 27’000.- CHF, mais son compte aura un solde total de 64’480.- CHF environ. Cela signifie que les intérêts générés réprésentent 58 % du capital total ! Tom a donc économisé plus d’argent grâce aux intérêts composés que de part sa propre épargne.
Si cela ne te convainc toujours pas, n’hésite pas à me contacter et je me ferai un plaisir d’échanger avec toi sur le sujet !
Conclusions
Que doit-on retenir de cet article ? Que sa soit de l’épargne classique avec des taux d’intérêts bas ou au mieux une prévoyance personnelle dans un 3a investi en bourse par exemple, mise à part que le rendement moyen espéré sera potentiellement très différent, les intérêts composés feront leur travail et seront de plus en plus efficace avec le temps. Le temps est la seule variable que tu ne peux pas contrôler. Tout au cours de ta vie, ton salaire va changer, ton potentiel de placement et donc d’épargne va augmenter et les taux d’intérêts vont fluctuer.
Si je devais donner un conseil à une personne qui n’a pas encore une vision claire de l’épargne personnelle, ce serai celui-ci :
« Commence à épargner (investir) maintenant ! Pas demain, mais aujourd’hui et fait-le régulièrement ! Peu importe le montant. Que tu mettes 50.- CHF / mois ou 3000.- CHF, ton argent doit travailler pour toi ! »
Il est évident que pour obtenir des taux de rendement de l’ordre de 5 % et plus, cela ne va pas se faire avec des comptes bancaires classiques type épargne ou salaire. Si tu veux atteindre ce genre d’objectif, tu devras obligatoirement te diriger vers des placements en bourse et le taux ne sera bien évidemment pas garanti. Cependant, les placements en bourse ne sont plus réservés aux élites et déjà riches. Un prochain article sera bientôt disponible à ce sujet. De toute manière, avant de te lancer dans des placements en bourse, je te conseille de mettre le maximum sur ton 3ème pilier 3a (6’883.- CHF en 2021). Je t’invite à aller lire mon article sur le sujet qui te permet de faire fructifier ton argent, tout en économisant des impôts.
Sources
1 : https://www.worldometers.info/fr/population-mondiale/


